研究内容
コンピュータを使って、物質中の電子の振る舞いを調べています。この際、 経験的なパラメータを使わない、"第一原理計算"が研究の中心です。 つまり物質を構成する原子核の原子番号と、その位置だけを与えて、その回りを運動する電子の状態を量子力学の方程式を解いて求めます。ここから、さまざまな物理量を計算して、実験と比較します。
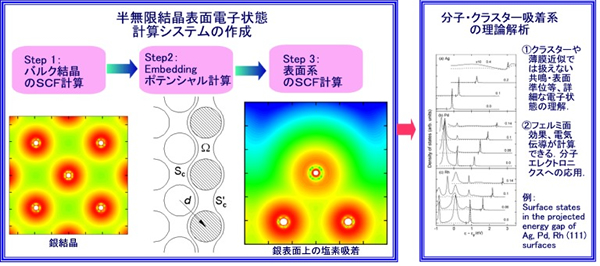
当研究室では、固体の表面や界面など、3次元結晶の欠陥を中心に扱っています。これらの系では対称性が低いため、これまで3次元結晶に対して発展してきた計算手法が使えなくなるのです。そこで、エムベッディッドGreen関数法を用いて、密度汎関数法の範囲で半無限の固体結晶表面・界面の電子の方程式を解くコンピュータのプログラムを開発しています。半無限の固体結晶表面の電子状態を、精度高く計算できる研究室は、世界中にもほとんどありません。
最近の研究から
■ トポロジカル絶縁体ナノリボンを用いたトランジスター
2次元トポロジカル絶縁体のナノリボンを並列接合した系を考え、バルクバンドギャップ中に生じる1次元エッジ状態によるバリスティック電流を計算しました。 左右のナノリボンの間に島状の領域をもうけ、この領域にゲート電圧をかけることにより、左右のナノリボン間を流れる電流の"on"と"off"状態を制御できることを示しました。 原理は簡単ですが、トポロジカル絶縁体を用いたトランジスターに応用できます。
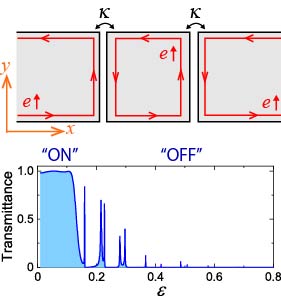
図 2次元トポロジカル絶縁体のナノリボンを使ったトランジスター
■ バンド絶縁体のZ2トポロジカル不変量
時間反転対称性を持つバンド絶縁体のZ2トポロジカル不変量が、エムベッディングポテンシャルの振舞いから容易に決められることを示しました。ブリルアンゾーン内の2個の時間反転不変運動量点kα、kβを結ぶバンドギャップ中の経路ε=ε0(k)に沿ってエムベッディングポテンシャルの固有値をグラフに描くと、両端点で固有値は2重に縮退したKramersペアを作ります。kαにおけるKramersペアが再び、kβでKramersペアを作る場合は自明な絶縁体(下左図)、kβでKramersペアの組み換えが起こる場合がトポロジカル絶縁体になります(下右図)。この方法により、バンドのパリティからZ2トポロジカル不変量を決められない空間反転対称性のない絶縁体においても、Z2トポロジカル不変量が容易に計算できることになります。
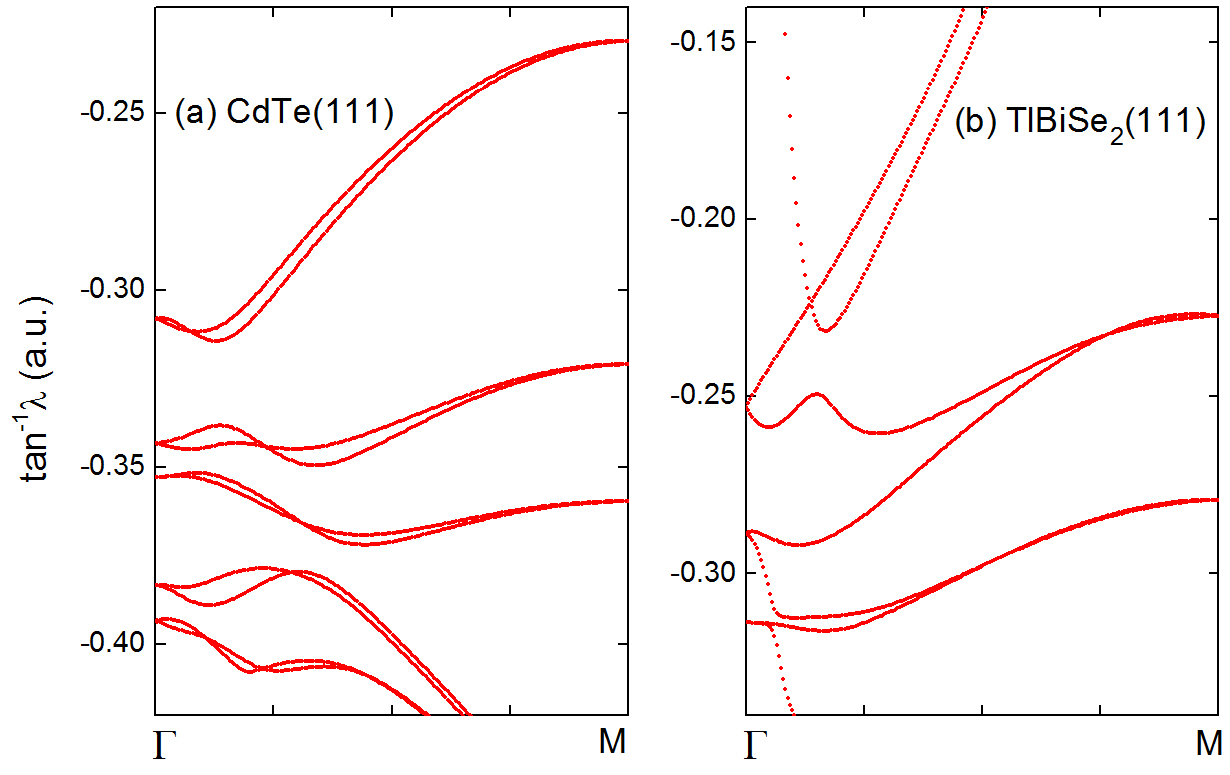
図 バンド絶縁体のエムベッディングポテンシャル固有値スペクトル(左:自明な絶縁体、右:トポロジカル絶縁体)
■ トポロジカル絶縁体/Mott絶縁体界面の電子構造
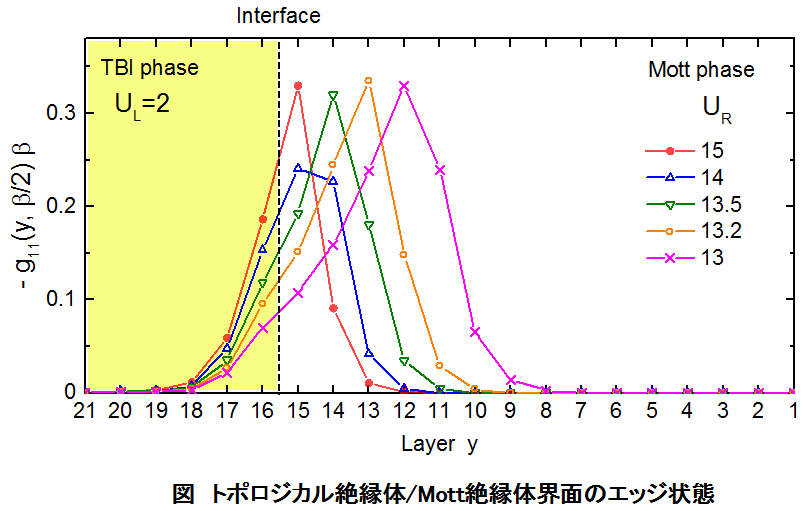
トポロジカルバンド絶縁体とMott絶縁体の界面の電子構造を、ハバード型のクーロン反発力を取り入れたBernevig-Hughes-Zhang(BHZ)模型と動的平均場理論(DMFT)を用いて計算しました。両相は同じ強さのスピン軌道相互作用を持っていますが、クーロン反発エネルギーの違いにより相転移を起こします。界面における近接効果により、Mott絶縁体の界面原子層がトポロジカル絶縁体に相転移して、その結果、トポロジカル絶縁体を特徴づける局在エッジ状態が、Mott絶縁体側の内部へ侵入することが分りました。
■ 金属表面バンドのRashba効果
非磁性体結晶のエネルギーバンドは、空間反転対称性があれば、スピン軌道相互作用の強さにかかわらず2重に縮退します。しかし、結晶表面では空間反転対称性が破れるため、表面局在バンドのエネルギー縮退が解けて分裂します(Rashba効果)。従来、密度汎関数法(DFT)によるRashba効果の計算の大部分は、結晶表面を薄膜モデルで近似して行われました。本研究室ではエムベッディッドGreen関数法による半無限結晶表面の第一原理DFT計算により、結晶表面のRashba効果を調べました。
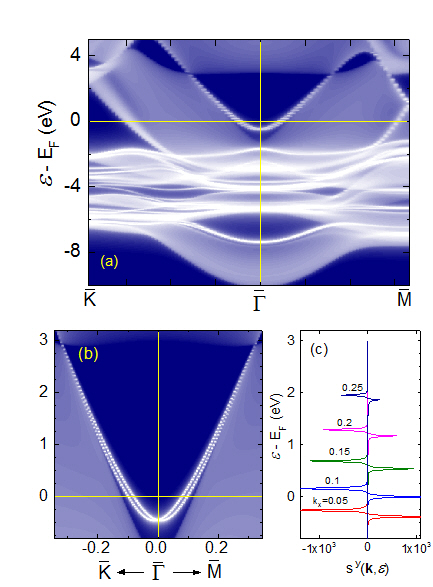
図 Au(111)表面のRashba効果
■ ハバード分子のクーロンブロッケードと近藤効果
金属電極間を架橋する単一分子の電気伝導度に対する電子相関の効果を調べるため、半無限2電極を架橋するHubbard分子を考え、バイアス電圧0の極限での電子構造を、温度の関数として調べました。分子共鳴準位は、Coulombブロッケードにより2つに分裂しますが、温度が低下すると近藤共鳴準位が出現して、このCoulombギャップが消失する様子を調べました。
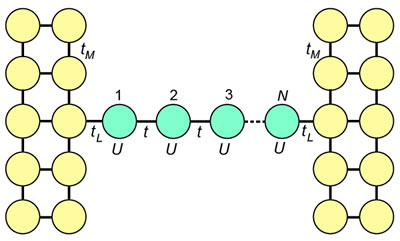
図 電極を架橋するハバード分子
■ 金属/Mott絶縁体界面の電子状態
強相関系を扱う理論手法として、動的平均場理論(DMFT)が広く用いられています。バルク結晶に関しては、隣接サイト間の電子相関を考慮したクラスターDMFT計算が標準的になりつつありますが、これまで表面・界面系の計算は、単一サイトDMFTに限られていました。本研究室では表面・界面系の電子構造をクラスターDMFTにより計算しました。
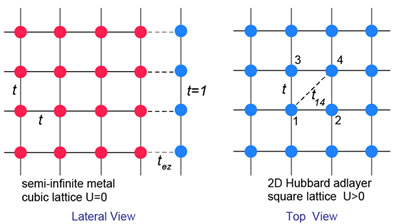
図 金属表面上のハバード吸着層
